Current Research

Monolithic Arbitrary Lagrangian-Eulerian (ALE) methods for shock hydrodynamics and multi-phase flow computations:
For flows with very strong shocks such as blast waves, Lagrangian methods have the advantage over Eulerian ones in that they provide much better resolution near shock fronts. However, these methods are vulnerable to mesh distortions that are usually due to, for example, strong compressive effects near the shock fronts or rotational flows. The Arbitrary Lagrangian-Eulerian (ALE) methods allow the mesh to move freely from the flow particles; and in the context of shock hydrodynamics this is achieved by first performing a Lagrangian step, then smoothing the grids, and transferring the data from the old grid to the smoothed one.
Despite its popularity in the past decades, the Lagrangian/Remap strategy suffers from the expensive data remap step, which usually involves a fundamentally different solution procedure to the Lagrangian flow solve, and the difficulty in treating incoming and outgoing flow boundaries, which typically means node insertion or deletion. To this end, a monolithic ALE method is proposed for shock hydrodynamics to overcome these issues. In particular, the mesh smoothing step is performed before the flow update; and the mesh velocity is incorporated in the governing equations that are solved by a nodal finite element method.
The key components of the proposed method are a variational multiscale (VMS) stabilization to enhance the linear stability and an entropy viscosity to capture strong shocks. Furthermore, the method is constructed in a way such that it reduces to the existing Lagrangian method when the mesh velocity is identical to the flow velocity; hence exact mass conservation is achieved in the Lagrangian limit. Application of the proposed method in various flow settings are depicted in the examples below.
Example 1: Mach 5 flow past a brick
(video)
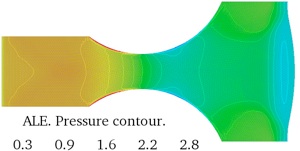
Example 2: ALE nozzle flow
(video)
Example 3: ALE five-point problem (a generalization of the Riemann problem to R^3)
(video)
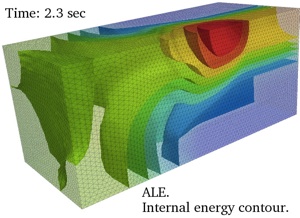
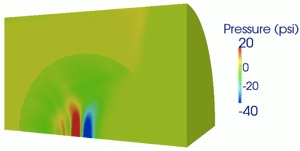
Example 4: Pressure contour in a planar-shock/soft gel interaction
(video)
Next, the monolithic ALE method is incorporated with the level set method and the ghost fluid method to construct an embedded boundary method, which is the first stage of extending the current methodology to multi-phase flow computations that involve very strong shocks and possible mesh motions. Currently, the extension is made to flow past fixed obstacles; and the ghost values is populated by solving a one-side Riemann problem exactly.
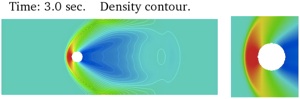
Example 5: Subsonic (upper) and supersonic (lower) past an embedded circular object
(video)
(video)
Extensions to flow past moving objects, two-phase flow computations, and multiple phase flows (more than three) with projected level set methods are on-going work.
Analysis and applications of a velocity/stress mixed stabilized nodal finite element for elastodynamics and wave propagations:
A new nodal mixed finite element method is proposed for the simulation of linear elastodynamics and wave propagations in the time domain. The method is based on equal-order interpolation of the velocity and the stress tensor: Galerkin least squares (GLS) or variational multiscale (VMS) stabilization are used for stabilization, and weak boundary conditions are used to enforce all the boundary conditions that include the interface between different materials. These development allows a stability proof of the proposed method on arbitrary complex domains. Particularly, the proof utilizes an equivalent form of the proposed method in the space/time domain, and shows the boundedness of a norm that incorporates both the state variables, their space/time residuals, and weakly enforced boundary contributions.
Example 1: Seismic wave past a rectangular domain

Example 2: Seismic wave past a complex domain

Example 3: Seismic wave past multiple layers of different geo-materials
Variational multiscale stabilized finite element methods of nodal tetrahedral elements for general transient solid dynamics and fluid-structure interactions:
An accurate, stable, and simple finite element method is developed for transient solid dynamics of various materials, which include both linear and nonlinear, elastic and inelastic, and compressible and nearly incompressible material models. In addition, the proposed method works for both tensorial elements and tetrahedral elements; thus it is suitable for computations involving any complex shapes.
The key concepts of the method is to write the rate-form equation for the volumetric stress, or the pressure variable of the system, and use the variational multiscale stabilization to deal with stiff responses caused by nearly incompressible responses.
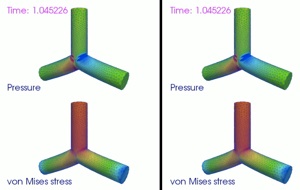
Example 1: Dynamics of a viscoelastic Y-connector (instant Poisson’s ratio = 0.499)
(video)
Example 2: Unstabilized (left) and stabilized (right) of the Taylor bar test of a complicate geometry
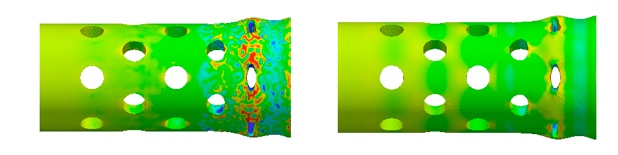
Example 3: A point-source blast wave inside a copper tank with internal support
(video)
Example 4: Interaction between a blast wave and a viscoelastic gel
(video)
A hybrid-variable method for general hyperbolic conservation laws:
A novel high-order methodology is proposed for general hyperbolic conservation laws. In the new framework, both the nodal variables and cell-averaged variables are used to discretize the governing equations in space; and these variables are evolved in time by the method of lines.
In the one-dimensional case, the method is shown to have an equivalent interpretation of simultaneous discretization of the original conservation law and the Hamilton-Jacobi equation for the integral of the sought solution. It is further shown that under a certain “generalized upwind” principle, the proposed method can be easily constructed to linearly stable and high-order accurate, at a much lower computational cost comparing to conventional finite-difference of finite-volume methods of the same order accuracy.
Example 1: Comparing the performance of first-order and second-order finite difference methods and a second-order HV (or FD-FV) method
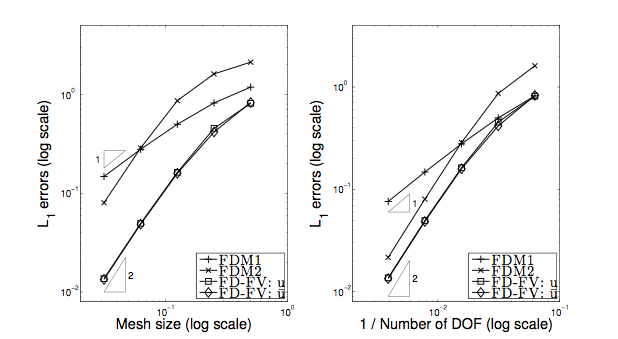

Example 2: Applying HV (or FD-FV) methods of up to fifth order of accuracy to solve a 1D Euler problem
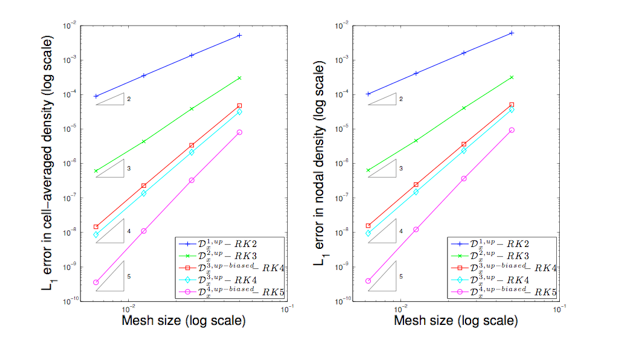
By using the tensor products of the 1D operators, the method is extended easily to Cartesian grids in multiple dimensions. Its extension to unstructured grids, however, is currently under investigation and has been constructed to second-order accuracy using a local coordinate transformation.
Example 3: A second-order HV (FD-FV) method to solve steady flow past a NACA 2412 airfoil

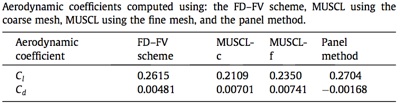
High-order embedded boundary methods for multi-material flow problems:
A new systematic approach is proposed to construct high-order embedded boundary methods for solving transport problems with dynamics boundaries in general and multi-material flow problems with moving material interfaces in particular. The idea of this new approach is to: (1) formally preserve the designed order of accuracy of the underlying flow solver near moving boundaries/interfaces; (2) employ exact multi-material Riemann solvers to enhance the stability of the coupling between different computational modules for each material.
For linear problems (advection/wave equations), up to third-order accurate finite-difference based embedded boundary methods are developed for Cartesian meshes in multiple dimensions. For Euler flow problems, the proposed methodology combines naturally with the FIVER framework to give a genuinely second-order embedded boundary methods to solve multi-material flow problems, in which the flows are solved by finite volume methods and the structures (if there is any) are solved by finite element methods. Unstructured grids in multiple dimensions are considered.
Example 1: 1D Euler problem -- 2nd-order MUSCL finite volume for gas; prescribed motion for piston
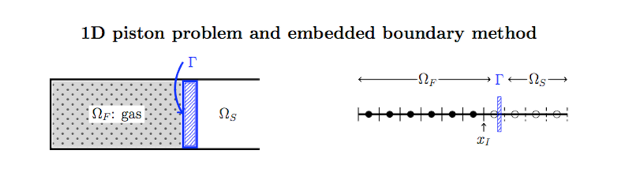
Example 2: Axisymmetric 2D Euler problem -- 2nd-order MUSCL finite volume for gas; prescribed motion for shrinking solid
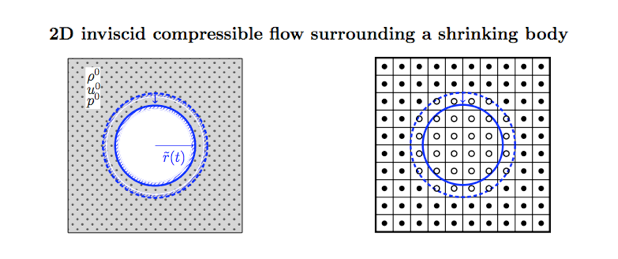
~ Solve the full 2D Euler problem: L1-norm: 1.92; Linf-norm: 1.78
~ Solve the 1D Euler problem w/ source: L1-norm: 1.98; Linf-norm: 2.12
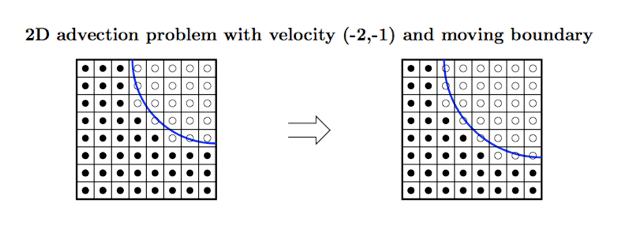
Example 3: 2D advection problem with moving boundary condition -- 3rd-order upwind finite difference

Recent Research
Enhanced slope limiter functions for cell-centered MUSCL schemes to solve hyperbolic conservation laws on irregular grids:
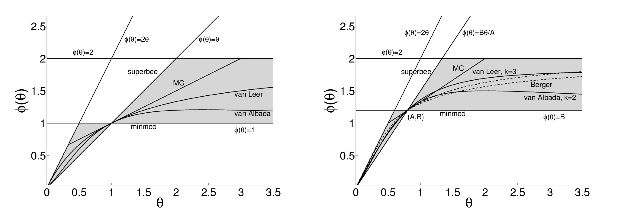
A general approach is proposed to study and enhance slope limiters in MUSCL type finite volume schemes on arbitrarily irregular grids. The enhancement ensures in 1D case: (1) nonlinear (TVD) stability; (2) formal second-order accuracy; (3) symmetry preserving property of the slope limiters even the grids is highly irregular. It is also shown that some most popular conventional slope limiters can never achieve these properties simultaneously whatever common smoothness monitors are used, unless the limiter function itself is modified. Extension to highly non-uniform Cartesian grids in multiple dimensions is achieved by tensor product of 1D operators.
The Sweby’s diagram for the conventional limiters (left) and the modified Sweby’s diagram for the proposed limiters (right):
Example 1: Advection of a step on an irregular grid

Test (b): MUSCL with modified slope and conventional limiter.
Test (c): MUSCL with conventional slope and proposed limiter.
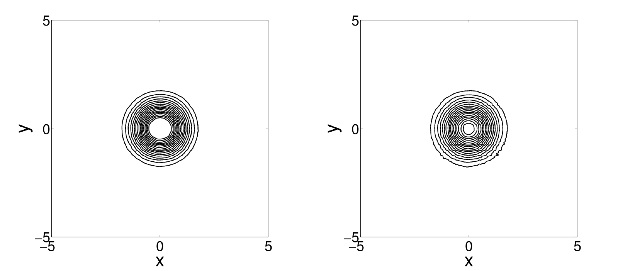
Example 2: Advection of a steady vortex on an irregular grid: Proposed limiter (left) and conventional limiter (right)
A frame-invariant flux-corrected remap method for vector fields in Lagrangian shock hydrodynamics.
A general procedure is proposed to transfer tensor fields in general and vector fields in particular between simplicial grids with the same connectivity. The method is based on the concept of algebraic flux-corrected transport (FCT), and it proofs to be monotone and objective (frame-invariance). The proposed method is applied to remap the velocity field in the context of Lagrangian shock hydrodynamics, and enables numerical simulation of strong shocks with rotational flows that cannot be performed before in the Lagrangian/Remap framework.
Example 1: Two dimensional Sedov problem on a quadrilateral grid
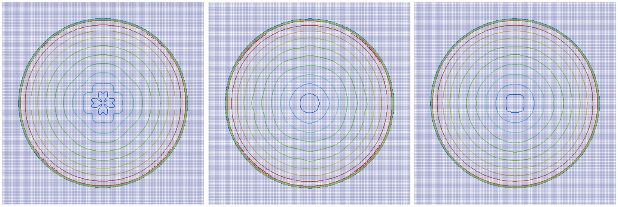
Middle: Apply the scalar limiter to each component of the velocity.
Right: Apply the proposed vector limiter to the velocity.
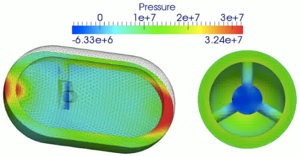
Example 2: Three dimensional Sedov problem on a hexahedral grid
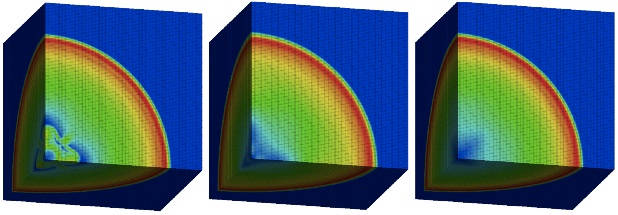
Middle: Apply the scalar limiter to each component of the velocity.
Right: Apply the proposed vector limiter to the velocity.
Example 3: Triple-point problem on a triangular grid

Middle: Apply the scalar limiter to each component of the velocity -- smeared vortex.
Right: Apply the proposed vector limiter to the velocity.
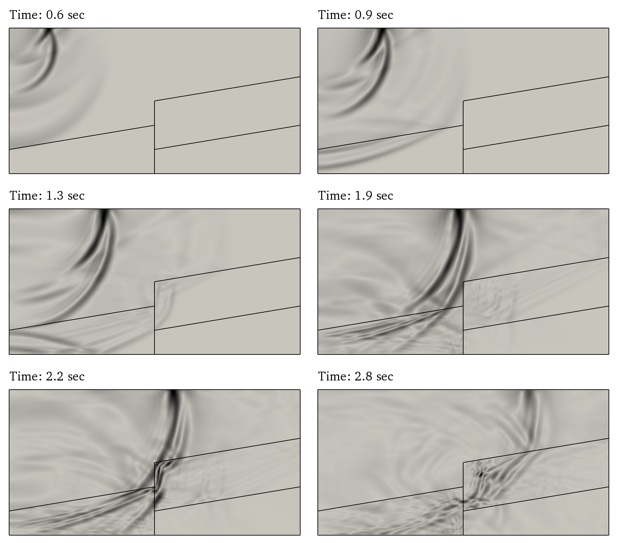
Example 4: Blast wave past a backward facing step
(video)
Past Research
Optimal design of agricultural landscape for pollination services.
Advised by: Professor Walter Murray
Computing inverse of block pentadiagonal matrices.
Advised by: Professor Gene Golub
Construction of high-degree irreducible polynomials on binary fields from lower-degree irreducible polynomials.
Advised by: Professor Maozhi Xu
Phylogeny estimation of a large number of sequences with high level of similarities.
Advised by: Professor Zhi Geng, Professor Songgang Li